1. DFT data
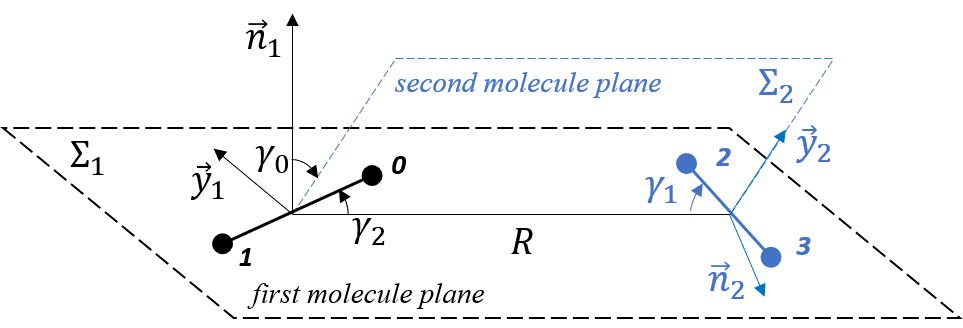
For each of the three types of interaction, DFT calculations were performed for the following mutual orientations of the molecules (see figure):
- R = {3A, 3.5A, 4A, … , 7.5A, 8A},
- γ_0 = {-90°, -80°, … , 80°, 90°},
- γ_1 = {5°, 15°, … , 75°, 85°},
- γ_2 = {0°, 10°, … , 80°, 90°}
Download DFT points: N2-N2.txt, N2-O2.txt, O2-O2.txt
2. Two-particle interaction model
An attempt was made to describe the potential energy surface (PES) obtained in the DFT calculations using pair interactions between the atoms of different molecules. This was done because this case of the interaction model is very simple and very convenient for trajectory MD calculations.
It was obtained that it is impossible to describe the interaction energy of the studied diatomic molecules using any two-particle interaction model with a mean-square relative discrepancy e_rel≲ 6% (even in the considered simplified case of rigid molecules). In this regard, below we tried to describe the obtained DFT points using the multi-particle interaction model.
Obtained mean-square relative discrepancy e_rel for two-particle fitting models
| ∆r, A | N2‒N2 | N2‒O2 | O2‒O2 |
| 0.1 | 7.86% Download | 5.8% Download | 5.74% Download |
| 0.025 | 7.61% Download | 5.5% Download | 5.58% Download |
3. Multi-particle interaction model
3.1. Model description
The potential was divided into the short-range (SR) and long-range (LR) parts: U = U_SR + U_LR. The SR part was U_SR = ∑ U_M(r_i), where U_M(r) = D*(e^(-2*α*(r-a)) - 2*e^(-α*(r-a))) ‒ Morse potential, α, a, D ‒ constants, r_i ‒ distances between atoms of different molecules. The LR part was written as a combination of trigonometric functions of the orientation angles: U_LR = A(R)*(∑ L_ijkl * F_i(γ_0) * F_j(γ_1) * F_k(γ_2) * G_l(R)), where L_ijkl ‒ constants, F_i(γ_j) ‒ i-th element of the set B_j = {1, cos(γ_j), sin(γ_j), cos(2*γ_j), sin(2*γ_j), …} for j = 0,1,2, G_i(R) ‒ i-th element of the set B_3 = {1, R^(-1), R^(-2), …}, N_j ‒ number of elements in the corresponding set B_j, A(R) = (R/R_0)^β exp(-β*R/R_0), where R_0, β ‒ constants.
Main characteristics of the proposed fitting models
| Model 1 | Model 2 | |||||
| Feature | N2‒N2 | N2‒O2 | O2‒O2 | N2‒N2 | N2‒O2 | O2‒O2 |
| α | 2.5 | 2 | 2.5 | 2 | 3.5 | 2.5 |
| β | 3 | 4 | 4 | 4 | 5 | 5 |
| R_0, A | 1.3 | 1.4 | 1.4 | 1.3 | 1.8 | 1.6 |
| Number of terms | 377 | 74 | ||||
| e_rel | 0.73% | 0.68% | 0.73% | 1.88% | 1.56% | 1.70% |
| K_j | Download | Download | Download | Download | Download | Download |
| Init file | m1-N2N2.txt | m1-N2O2.txt | m1-O2O2.txt | m2-N2N2.txt | m2-N2O2.txt | m2-O2O2.txt |
3.2. Model code (C++)
The described models and force field computation were implemented as a C++ code:
- C++ class for obtained potential - airpotentials.h
- Example of use - airlib.cpp
Before use, it is necessary to initialize the model from the file:
// Model class
airpotentials model;
// Init model from file
model.LoadModelFromFile("m1-N2N2.txt");
To calculate the energy and forces, it is necessary to call function ComputeEnergy(...) with the coordinates of the atoms and a pointer to the array into which the forces on the atoms will be stored:
// Atoms coordinates and forces
double x[4][3] = {...};
double f[4][3];
// Energy and forces computation
double U = model.ComputeEnergy(x,&f[0][0]);
Related Publication
A detailed description of the data posted here is presented in the paper:
Artem Yakunchikov, Vasily Kosyanchuk, Alexander Kroupnov, Michael Pogosbekian, Ilya Bryukhanov, Aliya Iuldasheva, Potential energy surface of interaction of two diatomic molecules for air flows simulation at intermediate temperatures // Chemical Physics, 536:110850, 2020. https://doi.org/10.1016/j.chemphys.2020.110850
Acknowledgments
The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University and Joint Supercomputer Center of the Russian Academy of Sciences. The research was supported by the Russian Foundation for Basic Research (project ¹ 18-31-20025).