Аннотация
Основными механизмами пластической деформация металлов является движение и размножение дислокаций и двойникование. Методом молекулярной динамики изучены механизмы зарождения и распространения петель частичных дислокаций в сплавах алюминия с медью. Исследован механизмы зарождения дислокаций в сплавах алюминия с медью и в присутствии зон Гинье-Престона. Показано методами молекулярно-динамического моделирования, что в сплавах образованию петли частичной дислокации предшествует образование наноразмерного локального структурного перехода ГЦК-ГПУ типа, в котором атомы сдвинуты друг относительно друга на половину величины вектора Бюргерса частичной дислокации. Показано, что частичная дислокация при распространении может трансформироваться в двойник или в полную дислокацию в зависимости от приложенного сдвигового напряжения. Получены зависимости скорости зарождения дислокаций от сдвигового напряжения в широком диапазоне температур вблизи примесных атомов меди и зон Гинье-Престона в алюминии. На основе рассчитанных данных построена модель релаксации сдвиговых напряжений в сплаве алюминия с медью. Показано, что зарождение дислокаций является основным механизмом пластической деформации при скоростях деформирования выше 107 c-1.
Материалы и результаты
При проведении молекулярно-динамических расчетов использовался пакет LAMMPS.
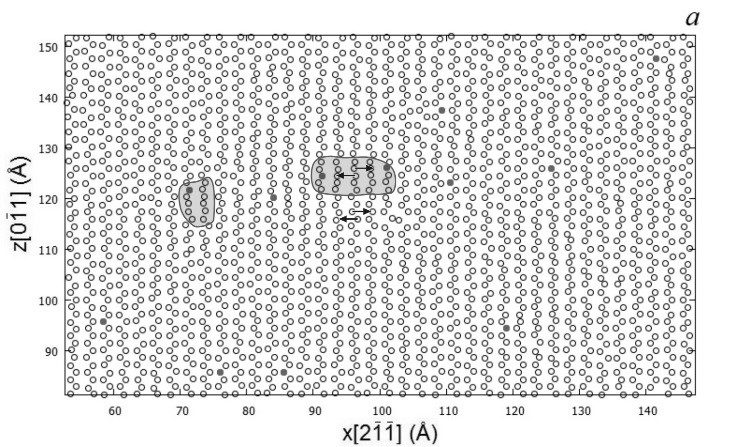
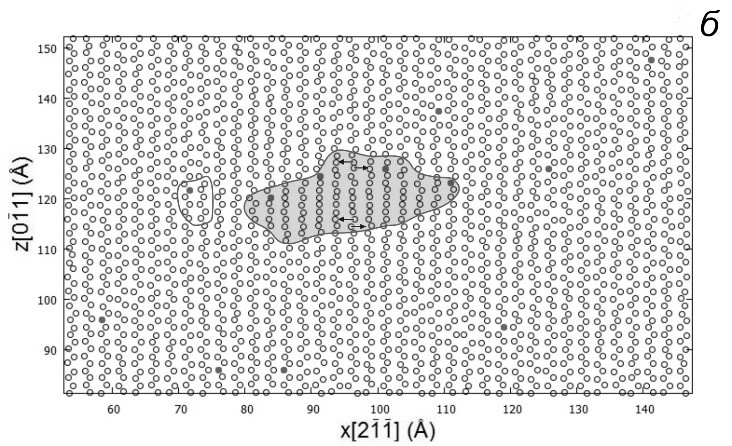
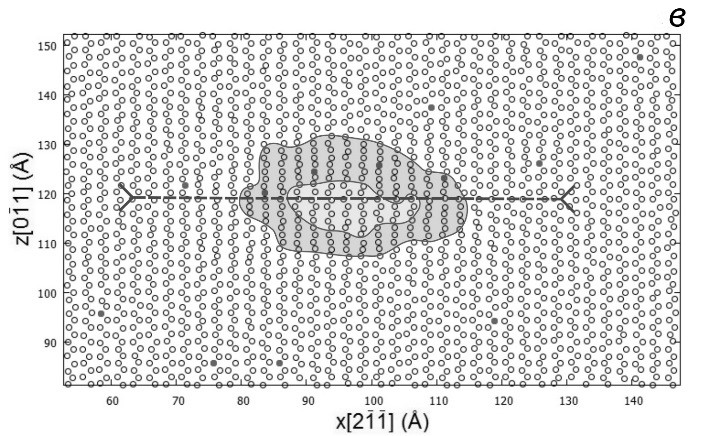
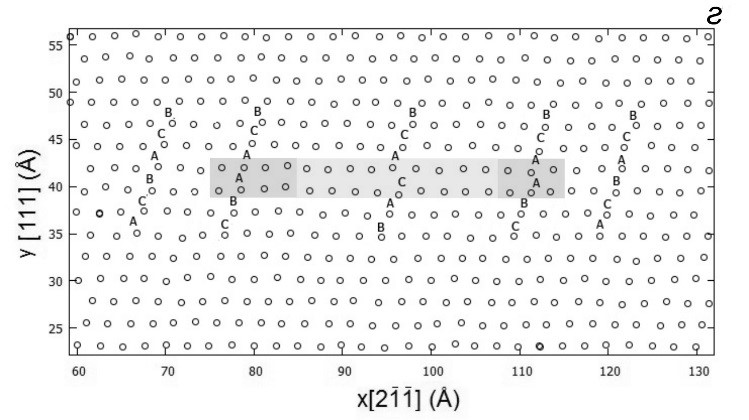
Рисунок 1. Зарождение и развитие дислокационной петли в сечениях xz (a-в) и xy (г) твердого раствора Al c 0.5% Cu при T = 300 К в моменты времени a – 40.3 пс, б – 40.7 пс, в и г – 41.7 пс. Прозрачные кружки – атомы алюминия двух ближайших плоскостей скольжения (111), в которых произошло зарождение, темные кружки – атомы меди Сu. Место сечения дислокационной петли (г) в плоскости xy указано стрелками на рис. 1в, буквами указаны атомные плоскости. Стрелками показано направление смещения атомов алюминия. Темно-серым цветом обозначены атомы дислокационного зародыша и ядра петли, светло-серым – атомы дефекта упаковки вычитания.
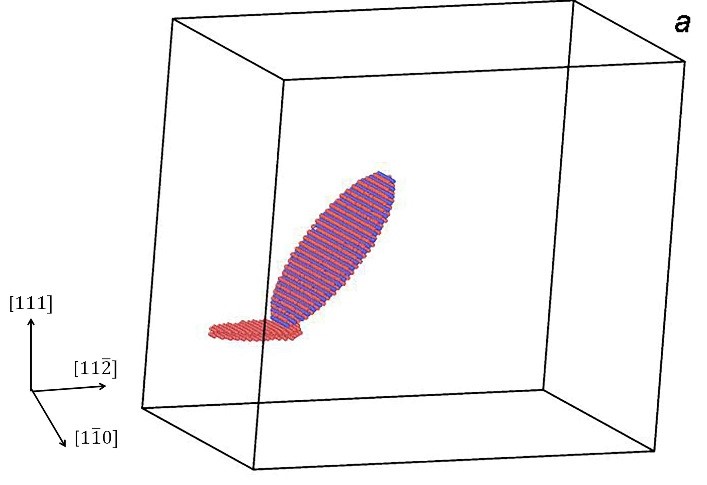
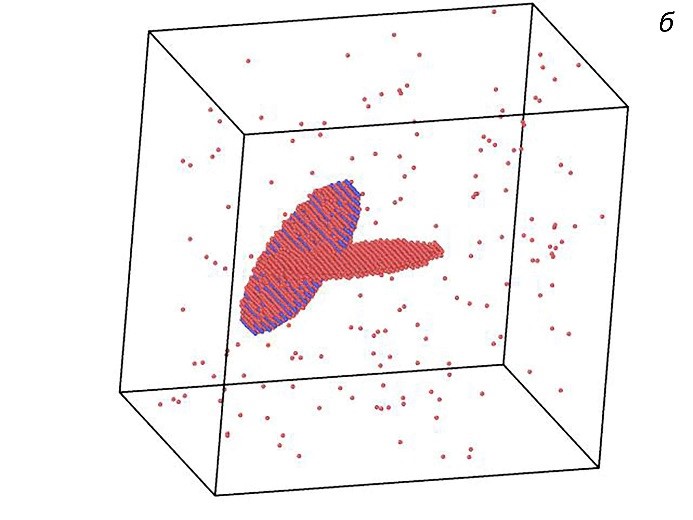
Рисунок 2. Два основных механизма зарождения дислокаций вблизи зоны Гинье-Престона (диаметр 3.5 нм). Красным цветом показаны атомы с дефектным локальным окружением, синим – атомы меди, образующие зону ГП. По первому механизму дислокационная петля зарождалась на краях зоны ГП (a), по второму – в середине плоскости зоны ГП (б).
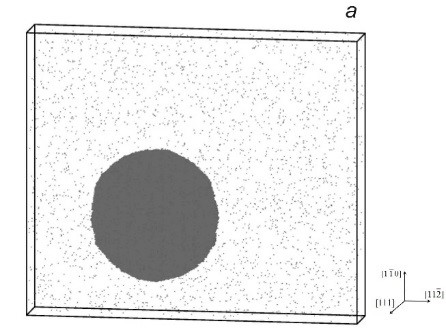
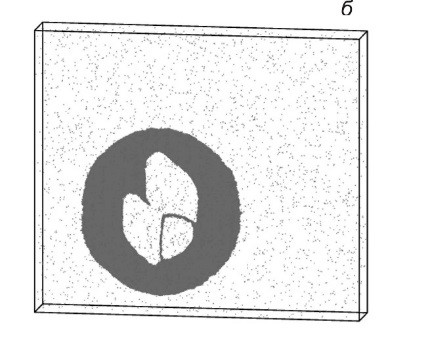
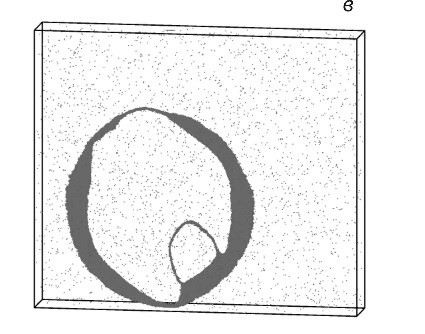
Рисунок 3. Образование петли полной дислокации из петли частичной дислокации в алюминии в моменты времени 10.5 пс (а), 16.2 пс (б), 20.5 пс (в) при температуре 300 К и напряжении 0.9 ГПа. Показаны чёрным атомы, значение параметра центросимметрии которых превышает 3.5.
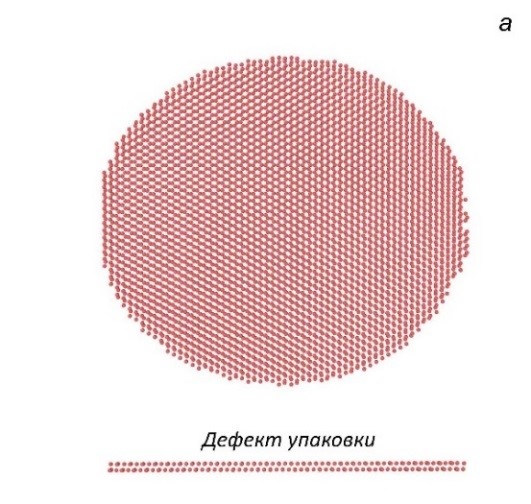

Рисунок.4. Образование двойника внутри движущейся петли частичной дислокации при 10 К в моменты времени 0.5 пс (а) и 1.0 пс (б) после создания петли. Фронт двойника представляет внешний дефект упаковки (ВДУ). Показан также и внутренний дефект упаковки (ДУ).
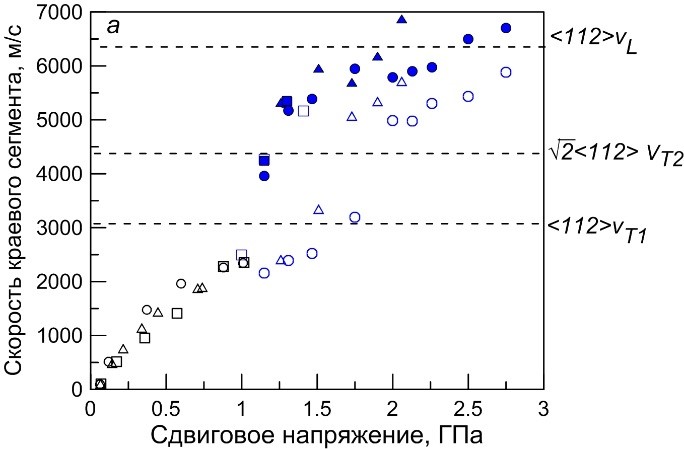
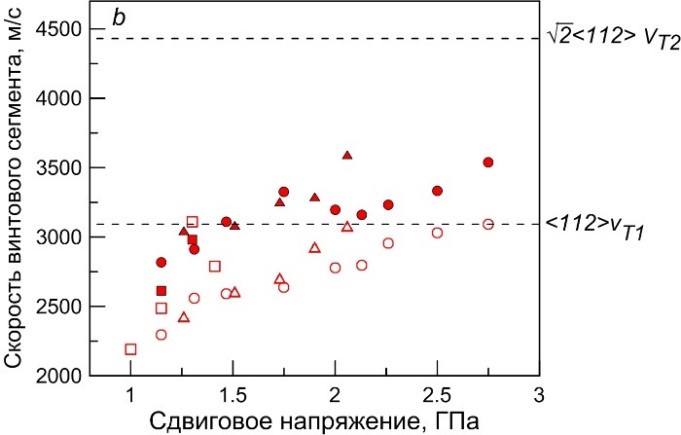
Рисунок 5. Зависимости скорости краевого (а) и винтового (б) сегмента от сдвигового напряжения при температурах 10 (круги), 300 (треугольники), 700 К (квадраты). Закрашенными символами показана начальная скорость двойника, образующегося внутри дислокационной петли. Черным цветом на рисунке (а) показаны результаты моделирования одиночной краевой дислокации.
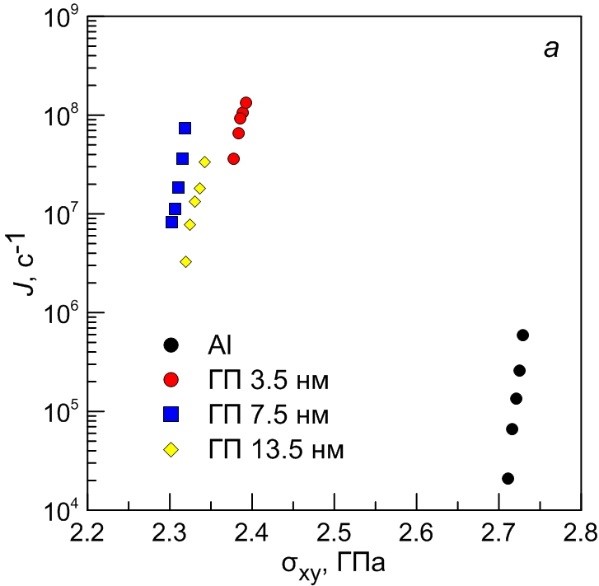
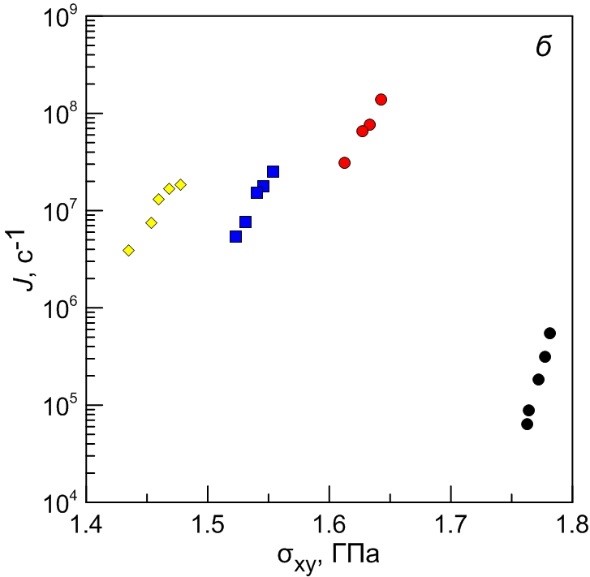
Рисунок 6. Зависимости скорости зарождения дислокаций, отнесенной к одному активационному центру, в чистом алюминии и в алюминии с зонами ГП при температурах 100 К (а) и 500 К (б).
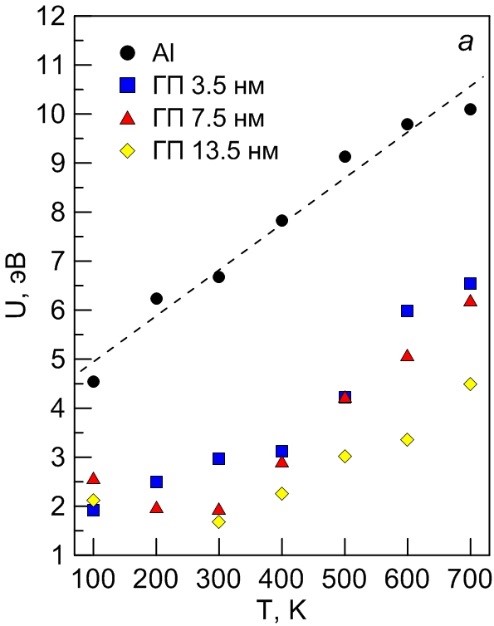
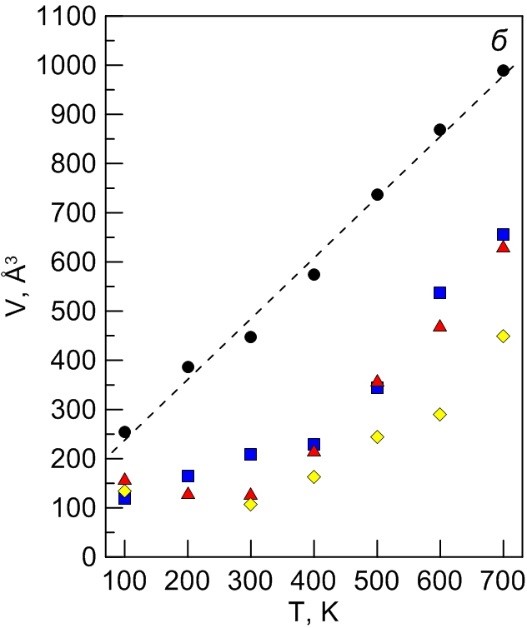
Рисунок 7. Зависимости энергии активации (а) и активационного объема (б) от температуры для чистого алюминия и алюминия с зонами ГП диаметра 3.5, 7.5 и 13.5 нм.
Модель релаксации сдвиговых напряжений в сплавах алюминия с медью: Рассматривалась модель сплава, в котором в начальный момент по всему объему в плоскостях (111) были расположены петли частичных дислокаций с заданной плотностью. Сдвиг системы осуществлялся вдоль вектора [112], как и в ранее проведенных МД расчетах. Полная деформация системы является суммой упругой и пластической.
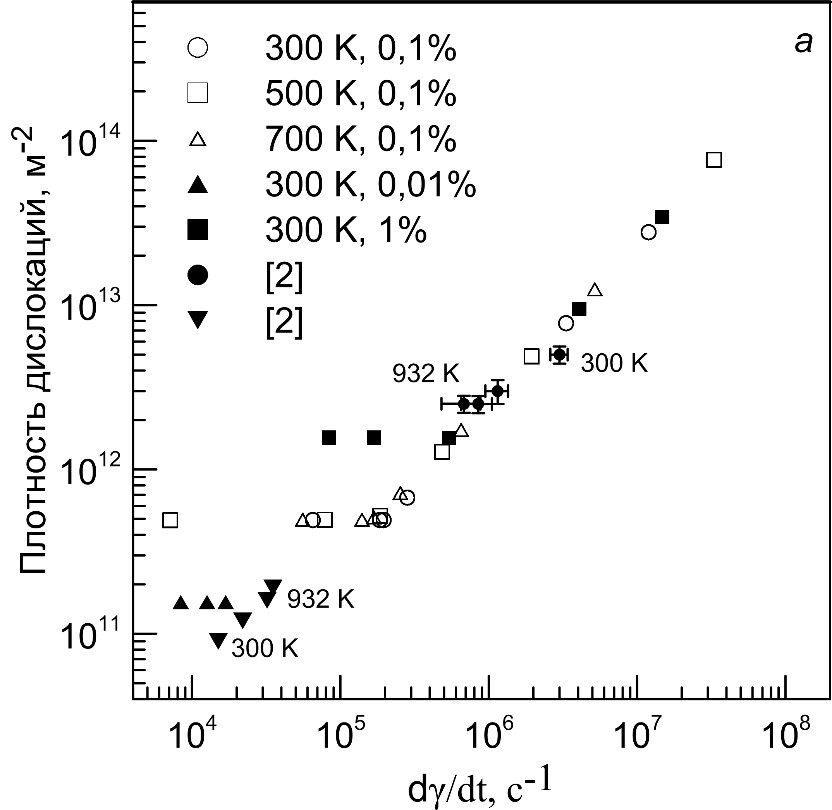
Рисунок 8. Результаты моделирования изменения плотности дислокаций со скоростью пластической деформации при различных температурах (300–700 К) и величинах пластической деформации (0,01–1%), полученные в настоящей работе, и экспериментальные значения плотности дислокаций в пластической волне (кружки), а также на упругом предвестнике (треугольники) в чистом алюминии.
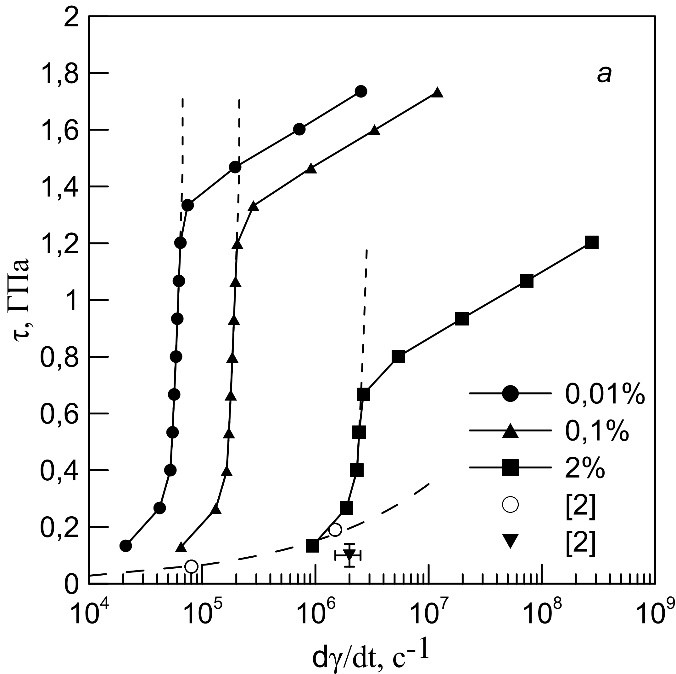
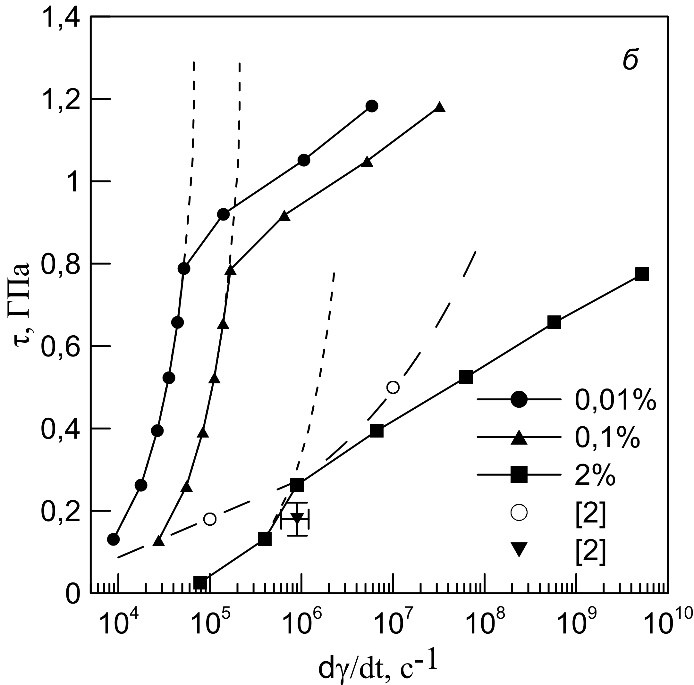
Рисунок 9. Зависимости сдвигового напряжения от скорости пластической деформации при 300 К (а) и 700 К (б) при пластических деформациях 0,01, 0,1 и 2%. Пунктирные линии – продолжение зависимостей без учета зарождения дислокаций; штрихпунктирные линии – экспериментальные зависимости сдвигового напряжения от скорости пластической деформации на упругом предвестнике (кружки) и в пластической волне (треугольники).
Публикации
- Брюханов И.А. Исследование релаксации сдвиговых напряжений в сплавах алюминия с медью на основе молекулярно-динамических расчетов. // Деформация и разрушение. – 2017. - №. 8. – С. 11-17.
- I.A. Bryukhanov, A.V. Larin Mechanisms and rate of dislocation nucleation in aluminum-copper alloys near Guinier-Preston zones. // Journal of Applied Physics. – 2016. – Т. 120. – №. 23. – С. 235106.
- Брюханов И.А., Ларин А.В. Молекулярно-динамическое моделирование процессов зарождения и развития частичных дислокаций в ГЦК металлах. // Фундаментальные проблемы современного материаловедения. – 2016. – Т. 13. – №. 4. – С. 517-521.
- Брюханов И.А., Ковалев В.Л., Ларин А.В. Зарождение дислокаций в сплавах алюминия с медью. // Физика твердого тела. – 2015. – Т. 57. – №. 9. – С. 1761-1771.